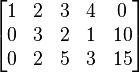Simplex algorithm

In mathematical optimization, Dantzig's simplex algorithm (or simplex method) is a popular algorithm for linear programming.The journal Computing in Science and Engineering listed it as one of the top 10 algorithms of the twentieth century .

Example

Consider the linear program

Minimize

$Z = -2 x - 3 y - 4 z\,$

Subject to

$\begin{align} 3 x + 2 y + z &= 10\\ 2 x + 5 y + 3 z &= 15\\ x,\, y,\, z &\ge 0 \end{align}$

This is represented by the (non-canonical) tableau

$\begin{bmatrix} 1 & 2 & 3 & 4 & 0 \\ 0 & 3 & 2 & 1 & 10 \\ 0 & 2 & 5 & 3 & 15 \end{bmatrix}$

Introduce artificial variables u and v and objective function W = u + v, giving a new tableau

$\begin{bmatrix} 1 & 0 & 0 & 0 & 0 & -1 & -1 & 0 \\ 0 & 1 & 2 & 3 & 4 & 0 & 0 & 0 \\ 0 & 0 & 3 & 2 & 1 & 1 & 0 & 10 \\ 0 & 0 & 2 & 5 & 3 & 0 & 1 & 15 \end{bmatrix}$

Note that the equation defining the original objective function is retained in anticipation of Phase II. After pricing out this becomes

$\begin{bmatrix} 1 & 0 & 5 & 7 & 4 & 0 & 0 & 25 \\ 0 & 1 & 2 & 3 & 4 & 0 & 0 & 0 \\ 0 & 0 & 3 & 2 & 1 & 1 & 0 & 10 \\ 0 & 0 & 2 & 5 & 3 & 0 & 1 & 15 \end{bmatrix}$

Select column 5 as a pivot column, so the pivot row must be row 4, and the updated tableau is

$\begin{bmatrix} 1 & 0 & \tfrac{7}{3} & \tfrac{1}{3} & 0 & 0 & -\tfrac{4}{3} & 5 \\ 0 & 1 & -\tfrac{2}{3} & -\tfrac{11}{3} & 0 & 0 & -\tfrac{4}{3} & -20 \\ 0 & 0 & \tfrac{7}{3} & \tfrac{1}{3} & 0 & 1 & -\tfrac{1}{3} & 5 \\ 0 & 0 & \tfrac{2}{3} & \tfrac{5}{3} & 1 & 0 & \tfrac{1}{3} & 5 \end{bmatrix}$

Now select column 3 as a pivot column, for which row 3 must be the pivot row, to get

$\begin{bmatrix} 1 & 0 & 0 & 0 & 0 & -1 & -1 & 0 \\ 0 & 1 & 0 & -\tfrac{25}{7} & 0 & \tfrac{2}{7} & -\tfrac{10}{7} & -\tfrac{130}{7} \\ 0 & 0 & 1 & \tfrac{1}{7} & 0 & \tfrac{3}{7} & -\tfrac{1}{7} & \tfrac{15}{7} \\ 0 & 0 & 0 & \tfrac{11}{7} & 1 & -\tfrac{2}{7} & \tfrac{3}{7} & \tfrac{25}{7} \end{bmatrix}$

The artificial variables are now 0 and they may be dropped giving a canonical tableau equivalent to the original problem:

$\begin{bmatrix} 1 & 0 & -\tfrac{25}{7} & 0 & -\tfrac{130}{7} \\ 0 & 1 & \tfrac{1}{7} & 0 & \tfrac{15}{7} \\ 0 & 0 & \tfrac{11}{7} & 1 & \tfrac{25}{7} \end{bmatrix}$

This is, fortuitously, already optimal and the optimum value for the original linear program is −130/7.

EXAMPLE (Part 1): Simplex method

Resolve using the Simplex Method the following problem:

Maximize	Z = f(x,y) = 3x + 2y
subject to:	2x + y ≤ 18
	2x + 3y ≤ 42
	3x + y ≤ 24
	x ≥ 0 , y ≥ 0

Are considerated the following phases:

1. Turning the inequalities into equalities

Introduce a slack variable for each restrictions of the type ≤ to turn them into equalities, giving the following linear equation system:

2x + y + r = 18

2x + 3y + s = 42

3x +y + t = 24

2. Equaling the objective function to zero

- 3x - 2y + Z = 0

3. Writing the initial board simplex

At columns will appear all basic variables of the problem and the slack/surplus variables. At rows you can observe, for each restriction the slack variables with its coefficients of obtained equalities, and the last row with the values resulting of substitute the value of every variable at function objetive, and operate just as was explained in the theory to get the left values from the row:

Board I . 1st iteration
			3	2	0	0	0
Base	Cb	P0	P1	P2	P3	P4	P5
P3	0	18	2	1	1	0	0
P4	0	42	2	3	0	1	0
P5	0	24	3	1	0	0	1
Z		0	-3	-2	0	0	0

4. Halt condition

When at the Z row there aren't negatives values , the optimal solution of the problem has been reached. In such a case, the algorithm has finished. If it were not so, the following steps must be executed.

5. Input-output base condition

A. First, we must know the variable that enters into the base. For it we choose that value's column that in the row the Z is the minor of the presents negatives values. In this case would be the variable x (P1) of coefficient - 3.

If two or more equal coefficients exist that obey the previous condition (tie case), then we will choose that variable that be basic.

The column of the variable that goes into the base is named pivot column (In green color).
Once the variable that goes into the base was obtained, we are in condition to deduce what will be the variable that goes out . For it, divide each independent term (P0) among the correspondent element of the pivot column, taking care that the result must be bigger than zero, and the minimum of this values is chosen.

In our case: 18/2 [=9] , 42/2 [=21] y 24/3 [=8]

If any less or equal to zero element exist, such divide will not be do, or if every elements that belongs to pivot column are zero we are in the case of unbounded solution, and the problem just would be finished (See theory).

The term of the pivot column that gives the lowest positive quotient in previous division, the 3, right now than 8 is the lower quotient, indicates the row of the slack variable that goes out the base, t (P5). This row is named the pivot row(In green color).

If two or more quotients are equals when they are being calculated (tie case), make a choice for a non basic variable (if possible).
At intersection of pivot row with pivot column we have the pivot element, 3.

6. Calculating the coefficients of the new board.

The new coefficients of the pivot row , t (P5), are obtained dividing all of the coefficients from such row among the pivot element, 3, that is the one necessary to turn into 1.

Following, with Gaussian reduction we do zeros the remainders terms of that column, with it we get the new coefficients from the other rows including that belong to the objective function row Z.

Also, it can be done in the following way:

Pivot row:

New pivot row = (Old pivot row) / (Pivot)

Remainders rows:

New row = (Old row) - (Coefficients from old row placed at incoming variable's colum) x (New pivot row)

Lets see an example, once the pivot row has been calculated (x's (P1) row at Board II):

Old row P4	42	2	3	0	1	0
	-	-	-	-	-	-
Coefficient	2	2	2	2	2	2
	x	x	x	x	x	x
New pivot row	8	1	1/3	0	0	1/3
	=	=	=	=	=	=
New row P4	26	0	7/3	0	1	-2/3

Board II . 2nd iteration
			3	2	0	0	0
Base	Cb	P0	P1	P2	P3	P4	P5
P3	0	2	0	1/3	1	0	-2/3
P4	0	26	0	7/3	0	1	-2/3
P1	3	8	1	1/3	0	0	1/3
Z		24	0	-1	0	0	1

Can be noticed that we have not attained the halt condition because at Z row, there is one negative, -1. We must do another iteration:

The incoming variable is y (P2), in order to be the variable that corresponds to the column where is the -1 coefficient.
B. To calculate the variable that goes out, we divide the terms from last column among the ones correspondent to the new pivot column: 2 / 1/3 [=6] , 26 / 7/3 [=78/7] and 8 / 1/3 [=24]
and as the lower positive quotient is 6, we have that the variable that goes out is r (P3).
The pivot element, that we must do it 1, is 1/3.

Working of analogous form that before, we obtain the board:

Board III . 3rd iteration
			3	2	0	0	0
Base	Cb	P0	P1	P2	P3	P4	P5
P2	2	6	0	1	3	0	-2
P4	0	12	0	0	-7	1	4
P1	3	6	1	0	-1	0	1
Z		30	0	0	3	0	-1

As you can see, there is a element with minus sign in Z row, - 1, it means that we have not come still to the optimal solution. It is necessary to repeat the process:

The variable that comes to the base is t (P5) , because is the variable that correspond to the -1 coefficient.
To calculate the variable that goes out, we divide the terms from the last colum among the terms correspondent from new pivot colum: 6/(-2) [=-3] , 12/4 [=3], and 6/1 [=6]
and like the lower positive quotient is 3, we get s (P4) as the variable that goes out from base.
The pivot element, that we must do it 1, is 4.

We get the board:

Board IV . 4th iteration
			3	2	0	0	0
Base	Cb	P0	P1	P2	P3	P4	P5
P2	2	12	0	1	-1/2	1/2	0
P5	0	3	0	0	-7/4	1/4	1
P1	3	3	1	0	3/4	-1/4	0
Z		33	0	0	5/4	1/4	0

As in the last row, all the coefficients are positive, then the halt condition is obey, getting the optimal solution.

The optimal solution is given by the Z value, at the column of the solution values, in this case: 33. In the same column, you can notice the point where it is reached, watching the rows correspondents to the decision variables that come at base:(x,y) = (3,12)

Mathematics

Wednesday, 12 September 2012

IGCSE PAST PAPERS (Maths)

Sunday, 9 September 2012

Simplex Method

Simplex algorithm

Example

EXAMPLE (Part 1): Simplex method

Popular Posts