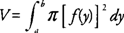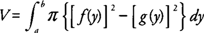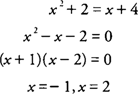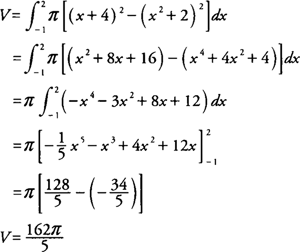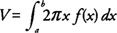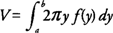Wednesday 20 June 2012

Website

List of A levels School in UAE

Thursday 14 June 2012

Radian is the ratio between the length of an arc and its radius.

Radian is now considered an SI derived unit.

The SI unit of solid angle measurement is the steradian.

The solid angle, Ω, is the two-dimensional angle in three-dimensional space that an object subtends at a point.

http://en.wikipedia.org/wiki/Solid_angle

As the ratio of two lengths, the radian is a "pure number" that needs no unit symbol, and in mathematical writing the symbol "rad" is almost always omitted.

An angle of 1 radian results in an arc with a length equal to the radius of the circle.

A complete revolution is 2π radians (shown here with a circle of radius one and circumference 2π).

Advantages of measuring in radians

In calculus and most other branches of mathematics beyond practical geometry, angles are universally measured in radians.

This is because radians have a mathematical "naturalness" that leads to a more elegant formulation of a number of important results.

Most notably, results in analysis involving trigonometric functions are simple and elegant when the functions' arguments are expressed in radians. For example, the use of radians leads to the simple limit formula

$\lim_{h\rightarrow 0}\frac{\sin h}{h}=1,$

which is the basis of many other identities in mathematics, including

$\frac{d}{dx} \sin x = \cos x$

http://en.wikipedia.org/wiki/Radian

$\frac{d^2}{dx^2} \sin x = -\sin x.$

Monday 11 June 2012

Limits in Calculus?

Limit

The limit of a function f(x) describes the behavior of the function close to a particular x value. It does not necessarily give the value of the function at x.

It is used in defining some of the more important concepts in calculus:

Continuity,
Derivative of a function, and
Definite integral of a function.

Volumes of Solids of Revolution

This type of solid will be made up of one of three types of elements—

Disks,
Washers, or
Cylindrical shells

—each of which requires a different approach in setting up the definite integral to determine its volume.

	Another version . . .
	Replay the animation

Disk method

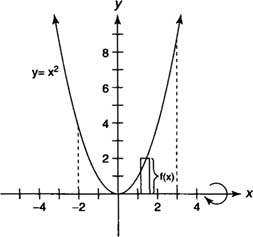
If the axis of revolution is the boundary of the plane region and the cross sections are taken perpendicular to the axis of revolution, then you use the disk method to find the volume of the solid. Because the cross section of a disk is a circle with area π r², the volume of each disk is its area times its thickness. If a disk is perpendicular to the x-axis, then its radius should be expressed as a function of x. If a disk is perpendicular to the y-axis, then its radius should be expressed as a function of y.
The volume ( V) of a solid generated by revolving the region bounded by y = f(x) and the x-axis on the interval [ a, b] about the x-axis is

If the region bounded by x = f(y) and the y-axis on [ a, b] is revolved about the y-axis, then its volume ( V) is

Note that f(x) and f(y) represent the radii of the disks or the distance between a point on the curve to the axis of revolution.
Example 1: Find the volume of the solid generated by revolving the region bounded by y = x² and the x-axis on [−2,3] about the x-axis. Because the x-axis is a boundary of the region, you can use the disk method (see Figure 1 ).

Figure 1

Diagram for Example 1.

The volume ( V) of the solid is

Washer method

If the axis of revolution is not a boundary of the plane region and the cross sections are taken perpendicular to the axis of revolution, you use the washer method to find the volume of the solid. Think of the washer as a “disk with a hole in it” or as a “disk with a disk removed from its center.” If R is the radius of the outer disk and r is the radius of the inner disk, then the area of the washer is π R² – π r², and its volume would be its area times its thickness. As noted in the discussion of the disk method, if a washer is perpendicular to the x-axis, then the inner and outer radii should be expressed as functions of x. If a washer is perpendicular to the y-axis, then the radii should be expressed as functions of y.
The volume ( V) of a solid generated by revolving the region bounded by y = f(x) and y = g(x) on the interval [ a, b] where f(x) ≥ g(x), about the x-axis is

If the region bounded by x = f(y) and x = g(y) on [ a, b], where f(y) ≥ g(y) is revolved about the y-axis, then its volume ( V) is

Note again that f(x) and g(x) and f(y) and g(y) represent the outer and inner radii of the washers or the distance between a point on each curve to the axis of revolution.
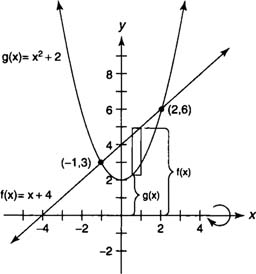
Example 2: Find the volume of the solid generated by revolving the region bounded by y = x² + 2 and y = x + 4 about the x-axis.
Because y = x² + 2 and y = x + 4, you find that

The graphs will intersect at (–1,3) and (2,6) with x + 4 ≥ x² + 2 on [–1,2] (Figure 2 ).

Figure 2

Diagram for Example 2.

Because the x-axis is not a boundary of the region, you can use the washer method, and the volume ( V) of the solid is

Cylindrical shell method

If the cross sections of the solid are taken parallel to the axis of revolution, then the cylindrical shell method will be used to find the volume of the solid. If the cylindrical shell has radius r and height h, then its volume would be 2π rh times its thickness. Think of the first part of this product, (2π rh), as the area of the rectangle formed by cutting the shell perpendicular to its radius and laying it out flat. If the axis of revolution is vertical, then the radius and height should be expressed in terms of x. If, however, the axis of revolution is horizontal, then the radius and height should be expressed in terms of y.
The volume ( V) of a solid generated by revolving the region bounded by y = f(x) and the x-axis on the interval [ a,b], where f(x) ≥ 0, about the y-axis is

If the region bounded by x = f(y) and the y-axis on the interval [ a,b], where f(y) ≥ 0, is revolved about the x-axis, then its volume ( V) is

Note that the x and y in the integrands represent the radii of the cylindrical shells or the distance between the cylindrical shell and the axis of revolution. The f(x) and f(y) factors represent the heights of the cylindrical shells.
Example 3: Find the volume of the solid generated by revolving the region bounded by y = x² and the x-axis [1,3] about the y-axis. In using the cylindrical shell method, the integral should be expressed in terms of x because the axis of revolution is vertical. The radius of the shell is x, and the height of the shell is f(x) = x² (Figure 3 ).

Figure 3

Diagram for Example 3.

The volume ( V) of the solid is

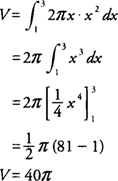Cliff Notes

Plane region

Replay the animation

Friday 8 June 2012

Combinations and Permutations

In English we use the word "combination" loosely, without thinking if the order of things is important. In other words:

	*"My fruit salad is a combination of apples, grapes and bananas"* We don't care what order the fruits are in, they could also be "bananas, grapes and apples" or "grapes, apples and bananas", its the same fruit salad.

	*"The combination to the safe was 472". Now we do care about the order. "724" would not work, nor would "247". It has to be exactly 4-7-2*.

So, in Mathematics we use more precise language:

	If the order doesn't matter, it is a Combination.
	If the order does matter it is a Permutation.

So, we should really call this a "Permutation Lock"!

In other words:

A Permutation is an ordered Combination.

Permutations

There are basically two types of permutation:

Repetition is Allowed: such as the lock above. It could be "333".
No Repetition: for example the first three people in a running race. You can't be first and second.

1. Permutations with Repetition

These are the easiest to calculate.

In other words, there are n possibilities for the first choice, THEN there are n possibilites for the second choice, and so on, multplying each time.

n × n × ... (r times) = n^r

Example: in the lock above, there are 10 numbers to choose from (0,1,..9) and you choose 3 of them:

10 × 10 × ... (3 times) = 10³ = 1,000 permutations

So, the formula is simply:

n^r

where n is the number of things to choose from, and you choose r of them
(Repetition allowed, order matters)

2. Permutations without Repetition

In this case, you have to reduce the number of available choices each time.

For example, what order could 16 pool balls be in?
After choosing, say, number "14" you can't choose it again.
So, your first choice would have 16 possibilites, and your next choice would then have 15 possibilities, then 14, 13, etc. And the total permutations would be:

16 × 15 × 14 × 13 × ... = 20,922,789,888,000

But maybe you don't want to choose them all, just 3 of them, so that would be only:

16 × 15 × 14 = 3,360

In other words, there are 3,360 different ways that 3 pool balls could be selected out of 16 balls.

where n is the number of things to choose from, and you choose r of them
(No repetition, order matters)

How many ways can first and second place be awarded to 10 people?

10!	=	10!	=	3,628,800	= 90

(10-2)!		8!		40,320

(which is just the same as: 10 × 9 = 90)

Combinations

There are also two types of combinations (remember the order does not matter now):

Repetition is Allowed: such as coins in your pocket (5,5,5,10,10)
No Repetition: such as lottery numbers (2,14,15,27,30,33)

web