LIMITS
| CENTRAL TO CALCULUS is the value of the slope of a line, | , but when |
| the terms become almost | 0 0 | . To evaluate the slope, that rate of change, |
under those vanishing conditions, requires the idea of a limit. And central to the idea of a limit is the idea of a sequence of rational numbers.
That is the idea of a sequence approaching a limit, or a boundary.
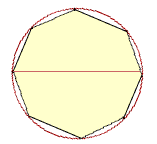
By that process we can approximate the value of π, which is the limit
of the ratio of perimeters to diameter, as closely as we care to.
By that process we can approximate the value of π, which is the limit
of the ratio of perimeters to diameter, as closely as we care to.
Problem 1. The student surely can recognize the number that is the limit of this sequence of rational numbers.
3, 3.1, 3.14, 3.141, 3.1415, 3.14159, 3.141592, . . .
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
To cover the answer again, click "Refresh" ("Reload").
π
We speak of a sequence as being infinite, which, in analogy with the sequence of natural numbers, is a brief way of saying that, no matter which term we name, there is a rule or a pattern that allows us to name one more.
1.9, 1.99, 1.999, 1.9999, 1.99999, . . .
Those values are getting closer and closer to 2 -- they are approaching 2 as their limit. 2 is the smallest number such that no matter which term of that sequence we name, it will be less than 2.
By "closer and closer" we mean the following. Choose an extremely small positive number. For example, "1 over the national debt(We say the absolute value because the terms are less than 2, and so the difference itself will be negative.)
When a variable x approaches a number l as a limit, we symbolize that as x
We also say that a sequence converges to a limit. The sequence above converges to 2.
Left-hand and right-hand limits
Now the sequence we chose were values less than 2. Hence we say that x approaches 2 from the left. We write
x  2−
2−
But we can easily construct a sequence of values of x that converges to 2 from the right; that is, a sequence of values that are more than 2.
For example,
For example,
2.2, 2.1, 2.01, 2.001, 2.0001, 2.00001, . . .
In this case, we write x  2+ .
2+ .
But again, no matter what small number we specify, if we go far enough out in that sequence, the value of a difference |x − 2| will be less than that small number. And so will all subsequent differences that we might name. Again, when we say that the values of x "approach a limit l," that limit is never a value of x as it approaches l. There is always a difference between the values of x and their limit. The limit is the boundary beyond which no member of the sequence will pass.
DEFINITION 2.1. The limit of a variable. We say that a sequence of values of a variable v approaches a limit l (a number which is not a term in the sequence) if, beginning with a certain term of the squence, the absolute value of v − l for that term and any subsequent term we might name is less than an extremely small positive number that we specify.
When that condition is satisfied, we write v  l.
l.
Thus if a sequence of values of a variable approaches a limit, there is always a difference between the limit and the terms of the sequence. But the difference becomes less than the specified small number of the definition, which is the error we are willing to tolerate. Therefore, because we specify that small number, we say that we can come as close to that limit as we please.
If Δx, then, is the variable that approaches the limit 0 (as it does when we determine the derivative), then Δx is never equal to 0.We have defined the limit of a variable, but what we typically have is a function of a variable -- which is also a variable. For example,
y = f(x) = x².
Now, a sequence of values of x will force a sequence of values of f(x). The question is: If the values of x approaches a limit, will the corresponding values of f(x) also approach a limit? If that is the case -- if f(x) approaches a limit L when x approaches a limit l -- then we write
"The limit of f(x) as x approaches l, is L."
In fact, let us see what happens to f(x) = x² as x  2−. Suppose again that x assumes this sequence of values:
2−. Suppose again that x assumes this sequence of values:
1.9, 1.99, 1.999, 1.9999, 1.99999, . . .
x² will then assume this sequence:
(1.9)², (1.99)²), (1.999)², (1.9999)², (1.99999)², . . .
It is easy to see that x² approaches 2² = 4.
Again, this means that, beginning with a certain term of the x² sequence, the absolute values of the differences between the terms and 4 will be less than any extremely small positive number that we might specify.
Moreover, if we consider a sequence x  2+:
2+:
2.2, 2.1, 2.01, 2.001, 2.0001, 2.00001, . . .
then x² becomes this sequence:
(2.2)², (2.1)², (2.01)² , (2.001)², (2.0001)², . . .
And that sequence also approaches 4. Therefore 4 is the limit of x² whether x approaches 2 from the right or from the left. And so we can drop the + or − signs and simply write:
To summarize:
function f(x) "has a limit" L as x approaches  , if for every sequence of values of x that approach
, if for every sequence of values of x that approach  as a limit (Definition 2.1) -- whether from the left or from the right -- the corresponding values of f(x) approach L as a limit (Definition 2.1).
as a limit (Definition 2.1) -- whether from the left or from the right -- the corresponding values of f(x) approach L as a limit (Definition 2.1).
If that is the case, then we write:
"The limit of f(x) as x approaches l is L."
In other words, for the limit of f(x) to exist as x approaches l , the left-hand and right-hand limits must be equal.
When we say, then, that a function has a limit, we mean that Definition 2.2 has been satified. In practice, it is not necessary to actually produce the requirements of the definition. The theorems on limits imply them.
The most important limit -- the limit that differential calculus is about -- is called the derivative. All the other limits studied in Calculus I are logical fun and games, never to be heard from again.
As x approaches 2 from the left, f(x) approaches 1. As x approaches 2 from the right, f(x) approaches 3. The left- and right-hand limits are not equal. Therefore, f(x) does not approach any limit as x approaches 2. Definition 2.2,
 value for
value for 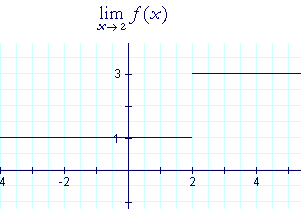
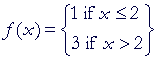
No comments:
Post a Comment