Math Tree O' Level

Math Topics Link Tree 
O' Level

Everyday Math

 Simple Interest (Flat Rates)

• Hire Purchase - Lease
• I = PRT /100
• 
  

Compound Interest

• %age Change

Matrices

• Simultaneous Equations
• Coordinates Geometry
• Vectors
• Transformation

Simultaneous Equations

• Matrices

Probability

• Identical
• Regular

Scale of Earth and Sun

Euclid as the Father of Geometry

Watch

M.Sc Mathematics

M.Sc Mathematics

Syllabus

AIOU

Semester – 1

1. Mathematical Applications with C ++
2. Topology
3. Ordinary Differential Equations
4. Differential Geometry
5. Advance Calculus

Semester – 2

1. Group Theory
2. Mechanics
3. Real Analysis
4. Linear Algebra
5. Complex Analysis

Semester – 3

1. Numerical Methods
2. Partial Differential Equations
3. Functional Analysis
4. Rings and Fields
5. Mathematical Statistics-1

Semester – 4

1. Operations Research
2. Combinatorics
3. Mathematical Statistics – 2
4. Mathematical Modeling
5. Research Report

Cone

Cone

 

In general, a cone is a pyramid with a circular cross section. 

A right cone is a cone with its vertex above the center of its base. 

However, when used without qualification, the term "cone" often means "right cone." 

In discussions of conic sections, the word "cone" is taken to mean "double cone," i.e., two cones placed apex to apex. The double cone is a quadratic surface, and each single cone is called a "nappe." The hyperbola can then be defined as the intersection of a plane with both nappes of the cone. 

Click

 

A Cone is a Rotated Triangle

Volume of a Cone vs Cylinder

  Click

Estimation and Rounding

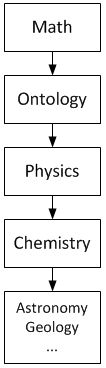
Math is an 'opportunity gateway.

Estimating

It is an important part of mathematics and a very handy tool for everyday life.

Rounding off is a kind of estimating.

Find the place value you want (the "rounding digit") and look at the digit just to the right of it.

In math, you can round up or round down.

Rounding up happens when you have a value that is half or greater of the amount you are rounding. Let's say you want to round to the nearest ten. If you were given the value 26, you would round up because 6 is greater than half of ten (5). If you were given 25, you would also round up. Rounding down happens when the value is less than half. Using the same examples, if you were given the number 24 you would round down because the four is less than five. Even if you were given the wacky decimal 24.9999, you would still round down because 4.9999 is less than five.

Here are some more examples:

Round 34 to the nearest 10 -- 30
Round 678 to the nearest 10 -- 680

It works for hundreds and thousands too.

Round 494 to the nearest 100 -- 500
Round 627 to the nearest 100 -- 600
Round 5,872 to the nearest 1,000 -- 6,000
Round 8,452 to the nearest 1,000 -- 8,000

Slides  


Significant Figures 

Slides 

GTE Practice Test

Powered by GreGuide Version 2.2.1 Copyrights 2007, GreGuide.com

Mechanics

Mechanics

Engineering Mechanics

Engineering Mechanics is divided into two: Statics and Dynamics.

Statics includes the following topics: resultant of force system; equilibrium of force system; cables; friction; trusses; frames; centroid; center of gravity; and moment of inertia.
Dynamics will cover the following topics: kinematics, dynamics, kinetics, work-energy equation, impulse and momentum, and mechanical vibrations.

• Principles of Statics
• Equilibrium of Force System
• Analysis of Structures
• Friction
• Centroids and Centers of Gravity
• Moment of Inertia and Radius of Gyration
• Dynamics

Principles of Statics

Statics is a branch of mechanics which studies the effects and distribution of forces of rigid bodies which are and remain at rest. In this area of mechanics, the body in which forces are acting is assumed to be rigid. The deformation of the body is treated in Mechanics and Strength of Materials.
Topics in Statics:

• Resultant of Force System
• Equilibrium of Force System
• Analysis of Trusses
• Cables
• Friction
• Centroids and Centers of Mass
• Moments of Inertia

• Components of a Force
• Moment of a Force
• Couples
• Resultant of Concurrent Force System
• Resultant of Parallel Force System
• Resultant of Non-Concurrent Force System

Advances in thermodynamics led to the development of industrialization; and

Advances in Mechanics inspired the development of calculus

Archimedes' screw, a simple machine for lifting

Engineering Mechanics

Mechanics (Greek) is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment.

The major division of the mechanics discipline separates:

• classical mechanics from
• quantum mechanics.

Classical mechanics originated with Isaac Newton's laws of motion in Principia Mathematica, while quantum mechanics didn't appear until 1900.

 Prof. Walter Lewin explains Newton's law of gravitation in MIT course 8.01

• Analytical mechanics
• Applied mechanics
• Dynamics
• Engineering
• Index of engineering science and mechanics articles
• Kinematics
• Kinetics
• Statics
• Wiesen Test of Mechanical Aptitude (WTMA)

Basic Mechanics

Classical Mechanics:



The following are described as forming Classical mechanics:

• Newtonian mechanics, the original theory of motion (kinematics) and forces (dynamics)
• Hamiltonian mechanics, a theoretical formalism, based on the principle of conservation of energy
• Lagrangian mechanics, another theoretical formalism, based on the principle of the least action
• Celestial mechanics, the motion of bodies in space: planets, comets, stars, galaxies, etc.
• Astrodynamics, spacecraft navigation, etc.
• Solid mechanics, elasticity, the properties of deformable bodies.
• Fracture mechanics
• Acoustics, sound ( = density variation propagation) in solids, fluids and gases.
• Statics, semi-rigid bodies in mechanical equilibrium
• Fluid mechanics, the motion of fluids
• Soil mechanics, mechanical behavior of soils
• Continuum mechanics, mechanics of continua (both solid and fluid)
• Hydraulics, mechanical properties of liquids
• Fluid statics, liquids in equilibrium
• Applied mechanics, or Engineering mechanics
• Biomechanics, solids, fluids, etc. in biology
• Biophysics, physical processes in living organisms
• Statistical mechanics, assemblies of particles too large to be described in a deterministic way
• Relativistic or Einsteinian mechanics, universal gravitation

Quantum mechanics

The following are categorized as being part of Quantum mechanics:

• Particle physics, the motion, structure, and reactions of particles
• Nuclear physics, the motion, structure, and reactions of nuclei
• Condensed matter physics, quantum gases, solids, liquids, etc.
• Quantum statistical mechanics, large assemblies of particles

Professional organizations

• Applied Mechanics Division, American Society of Mechanical Engineers
• Fluid Dynamics Division, American Physical Society
• Institution of Mechanical Engineers is the United Kingdom's qualifying body for Mechanical Engineers and has been the home of Mechanical Engineers for over 150 years.
• International Union of Theoretical and Applied Mechanics

This parabola-shaped lava flow illustrates the application of Mathematics in Physics – in this case,

Galileo's law of falling bodies


The distinction between Mathematics and Physics is clear-cut,
but not always obvious, especially in Mathematical Physics



Mathematics and Ontology are used in Physics.
Physics is used in Chemistry and Cosmology



Physics involves modeling the natural world with theory, usually quantitative. Here, the path of a particle is modeled with the mathematics of calculus to explain its behavior: the purview of the branch of physics known as mechanics

Physics 1
Mechanics Overview

Mechanics is the branch of Physics dealing with the study of motion. 

No matter what your interest in science or engineering, mechanics will be important for you - motion is a fundamental idea in all of science.

Mechanics can be divided into 2 areas - 

1. kinematics, dealing with describing motions, and 
2. dynamics, dealing with the causes of motion.

Physics 1 Mechanics topics include:

• Kinematics
  • Kinematics (in One Dimension)
  • Projectile Motion
• Dynamics
  • Newton's Laws
  • Momentum and Conservation of Momentum (in One Dimension)
  • Energy and Conservation of Energy
  
  

  Common phrases or words used in questions
• particle: a point mass
• body: same as a particle (not of the human variety)
• light inextensible string: a string with negligible mass that does not stretch

Guide lines on resolving:

Always aim to resolve in the direction that an object is moving.

If it is moving up a plane, resolve up the plane, if it is moving down the plane then resolve down the plane.

If you resolve in the opposite direction to motion then you will generally find yourself getting into all sorts of problems over acceleration having to be negative.

State the direction you are resolving by using R(left), R(up the plane) etc. Arrows inside the brackets can be used. It makes it clear to the person marking your work what you are intending to do.

Tutorial and Vedios 

Simple machine

A simple machine is a mechanical device that changes the direction or magnitude of a force. In general, they can be defined as the simplest mechanisms that provide mechanical advantage (also called leverage).

Usually the term refers to the six classical simple machines which were defined by Renaissance scientists:

• Lever
• Wheel and axle
• Pulley
• Inclined plane
• Wedge
• Screw

A simple machine is an elementary device that has a specific movement (often called a mechanism), which can be combined with other devices and movements to form a machine.

Between the simple machines and complex assemblies, several intermediate classes can be defined, which may be termed "compound machines" or "machine elements".

The mechanical advantage of a compound machine is simply the product of the mechanical advantages of the simple machines of which it is composed.

Probability

Probability


One of the important steps you need to make when considering the probability of two or more events occurring. Is to decide whether they are independent or related events.

Mutually Exclusive vs. Independent

It is common for people to confuse the concepts of mutually exclusive events and independent events.

Definition of a mutually exclusive event

If event A happens, then event B cannot, or vice-versa. The two events "it rained on Tuesday" and "it did not rain on Tuesday" are mutually exclusive events. When calculating the probabilities for exclusive events you add the probabilities.

Independent events
The outcome of event A, has no effect on the outcome of event B. Such as "It rained on Tuesday" and "My chair broke at work". When calculating the probabilities for independent events you multiply the probabilities. You are effectively saying what is the chance of both events happening bearing in mind that the two were unrelated.

So, if A and B are mutually exclusive, they cannot be independent. If A and B are independent, they cannot be mutually exclusive.

If the events we chose were it rained today" and "I left my umbrella at home" they are not necessarily mutually exclusive, but they are probably not independent either, because one would think that you'd be less likely to leave your umbrella at home on days when it rains.

Example of a mutually exclusive event

What happens if we want to throw 1 and 6 in any order?
This now means that we do not mind if the first die is either 1 or 6, as we are still in with a chance. But with the first die, if 1 falls uppermost, clearly It rules out the possibility of 6 being uppermost, so the two Outcomes, 1 and 6, are exclusive. One result directly affects the other. In this case, the probability of throwing 1 or 6 with the first die is the sum of the two probabilities, 1/6 + 1/6 = 1/3.

The probability of the second die being favourable is still 1/6 as the second die can only be one specific number, a 6 if the first die is 1, and vice versa.

Therefore the probability of throwing 1 and 6 in any order with two dice is 1/3 x 1/6 = 1/18. Note that we multiplied the the last two probabilities as they were independent of each other!!!

Example of an independent event

The probability of throwing a double three with two dice is the result of throwing three with the first die and three with the second die. The total possibilities are, one from six outcomes for the first event and one from six outcomes for the second, Therefore (1/6) * (1/6) = 1/36th or 2.77%.
The two events are independent, since whatever happens to the first die cannot affect the throw of the second, the probabilities are therefore multiplied, and remain 1/36th.

Mutually Exclusive: can't happen at the same time.

Examples:

• Turning left and turning right are Mutually Exclusive (you can't do both at the same time)
• Tossing a coin: Heads and Tails are Mutually Exclusive
• Cards: Kings and Aces are Mutually Exclusive

What is not Mutually Exclusive:

• Turning left and scratching your head can happen at the same time

P(A and B) = 0   impossible

But the probability of A or B is the sum of the individual probabilities:

P(A or B) = P(A) + P(B)

Example: Scoring Goals

If the probability of:

• scoring no goals (Event "A") is 20%
• scoring exactly 1 goal (Event "B") is 15%

Then:

• The probability of scoring no goals and 1 goal is 0 (Impossible)
• The probability of scoring no goals or 1 goal is 20% + 15% = 35%

Which is written:

P(A ∩ B) = 0

P(A ∪ B) = 20% + 15% = 35%

Not Mutually Exclusive

P(A or B) = P(A) + P(B) - P(A and B)

 

 

 

 

List of Text books 2010-2011 for A Level (CIE)

List of Text books 2010-2011 

for 

A Level (CIE)

Read

A Level Accounting

A Level Accounting
Author: Randall, Harold