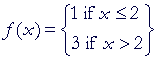these basic habits or principles that can keep your math teaching on the right track.
Habit 1: Let It Make Sense
Habit 2: Remember the Goals
Habit 3: Know Your Tools
Habit 4: Living and Loving Math
Habit 1: Let It Make Sense
Let us strive to teach for understanding of mathematical concepts and procedures, the
"why" something works, and not only the "how".
This understanding, as I'm sure you realize, doesn't always come immediately. It may take even several years to grasp a concept. For example, place value is something kids understand partially at first, and then that deepens over a few years.
This is why many math curricula use spiraling: they come back to a concept the next year, and the next. And this can be very good if not done excessively (like for 5-6 years is probably excessive).
However, spiraling also has its own pitfalls: if your child doesn't get a concept,
don't blindly "trust" the spiraling and think, "Well, she gets it the next year when the book comes back around to it."
The next year's schoolbook won't necessarily present the concept at the same level - the presentation might be too difficult. If a child doesn't "get it", they might need a very basic instruction for the concept again.
The
"how" something works is often called
procedural understanding: the child knows how to work long division, or the procedure of fraction addition or fraction division, for example. It is often possible to learn the "how" mechanically without understanding why it works. Procedures learned this way are often forgotten very easily.
The relationship between the "how" and the "why" - or between procedures and concepts - is complex.
One doesn't always come totally before the other, and it also varies from child to child. And, conceptual and procedural understanding actually help each other: conceptual knowledge (understanding the "why") is important for the development of procedural fluency, while fluent procedural knowledge supports the development of further understanding and learning.
Try alternating the instruction: teach how to add fractions, and let the student practice. Then explain why it works. Go back to some practice. Back and forth. Sooner or later it should 'stick' - but it might be next year instead of this one, or after 6 months instead of in this month.
As a rule of thumb, don't totally leave a topic until the student both knows "how", and understands the "why".
Tip: you can often test a student's understanding of a topic by asking HIM to produce an example, preferably with a picture or other illustration: "Tell me an example of multiplying fractions by whole numbers, and draw a picture." Whatever gets produced can tell the teacher a lot about what has been understood.
Habit 2: Remember the Goals
What are the goals of your math teaching? Are they...
- to finish the book by the end of school year
- make sure the kids pass the test ...?
Or do you have goals such as:
- My student can add, simplify, and multiply fractions
- My student can divide by 10, 100, and 1000.
These are all just "subgoals". But
what is the ultimate goal of learning school mathematics?
Consider these goals:
- Students need to be able to navigate their lives in this ever-so-complex modern world.
This involves dealing with taxes, loans, credit cards, purchases, budgeting, shopping. Our youngsters need to be able to handle money wisely. All that requires good understanding of parts, proportions, and percents.
- Another very important goal of mathematics education as a whole is to enable the students to understand information aroud us. In today's world, this includes quite a bit of scientific information. Being able to read through it and make sense of it requires knowing big and small numbers, statistics, probability, percents.
- And then one more. We need to prepare our students for further studies in math and science. Not everyone ultimately needs algebra, but many do, and teens don't always know what profession they might choose or end up with.
- I'd like to add one more broad goal of math education: teaching deductive reasoning. Of course geometry is a good example of this, but when taught properly, other areas of school math can be as well.
- Then one more goal that I personally feel fairly strongly about: let students see some beauty of mathematics and learn to like it, or at the very least, make sure they do not feel negatively about mathematics.
The more you can keep these big real goals in mind, the better you can connect your subgoals to them. And the more you can keep the goals and the subgoals in mind, the better teacher you will be.
For example, adding, simplifying, and multiplying fractions all connects with a broader goal of understanding parts or part and whole. It will soon lead to ratios, proportions, and percent. Also, all fraction operations are a needed basis for solving rational equations and doing the operations with rational expressions (during algebra studies).
Tying in with the goals, remember that the BOOK or CURRICULUM is just a tool to achieve the goals -- not a goal in itself. Don't ever be a slave to any math book.
Habit 3: Know Your Tools
Math teacher's tools are quite numerous nowadays.
First of all of course comes a black or white board, or paper - something to write on, pencil, compass, protractor, ruler, eraser.
And the book you're using.
Then we also have computer software, animations and activities online, animated lessons and such.
There are workbooks, fun books, worktexts, online texts.
Then all the manipulatives,
abacus, measuring cups, scales, algebra tiles, and so on.
And then there are games,
games, games.
The choices are so numerous it's daunting. What's a teacher to do?
Well, you just have to get started somewhere, probably with the basics, and then add to your "toolbox" little by little as you have opportunity.
There is no need to try 'hog' it all at once. It's important to
learn how to use any tool you might acquire. Quantity won't equal quality. Knowing a few "math tools" inside out is more beneficial than a mindless dashing to find the newest activity to spice up your math lessons.
Basic tools
- The board and/or paper to write on. Essential. Easy to use.
- The book or curriculum. Choosing a math curriculum is often difficult for homeschoolers. Check my curriculum pages for some help. Two things to keep in mind:
i) Now matter what book you're using, YOU as the teacher have the control. Don't be a slave to the curriculum. You can skip pages, rearrange the order in which to teach the material, supplement it, and so on.
ii) Don't despair if the book you're using doesn't seem to be the perfect choice for your student. You can quite likely sell it on homeschool swap boards, and buy some other one.
- Manipulatives. I once saw a question asked by a homeschooling parent, on the lines, "What manipulatives must I use and when?" The person was under the impression that manipulatives are a 'must' thing.
Manipulatives are definitely emphasized in these days. They are usually very good, but they're not the end goal of math education, and there is no need to go hog wild over them.
Manipulatives are something the student manipulates with his hands to get a better grasp of something. But the goal is to learn to do math without them.
Some very helpful manipulatives are
- A 100-bead basic abacus
- something to illustrate hundreds/tens/ones place value. I made my daughter ten-bags by putting marbles into little plastic bags.
- some sort of fraction manipulatives. You can just make pie models out of cardboard, even.
Often, drawing pictures can take place of manipulatives, especially after the first few grades and on.
Check out also some virtual manipulatives.
- Geometry and measuring tools. These are pretty essential, I'd say. For geometry however, dynamic software can these days replace compass and ruler and easily be far better.
The extras
These are, obviously, too many to even start listing.
- Some game or games are good for drilling basic facts. Games are nice for about any topic. Here's one that I played with playing cards with my dd; and now she seems to have learned the sums that add to 10. And here's a game that's worth 1000 worksheets. Of course the internet is full of online math games.
- I would definitely use some math software if teaching graphing, algebra, or calculus. Check MathProf for example, or Math Mechanixs. I've listed a few more here.
- If you're ready to add something new to your toolbox from the online world, try The Math Forum's MathTools - a library of technology tools, lessons, activities, and support materials. Check also my pages listing math games and activities online.
Habit 4: Living and Loving Math
You are the teacher. You show the way - also with your attitudes, your way of life.
Do you use math often in your daily life? Is using mathematical reasoning, numbers, measurements, etc. a natural thing to you every day?
And then: do you like math? Love it? Are you happy to teach it? Enthusiastic?
Both of these tend to show up in how you teach, but especially so in a homeschooling enviroment, because at home you're teaching your kids a way of life, and if math is a natural part of it or not.
Math is not a drudgery, nor something just confined to math lessons.
Some ideas:
- Let it make sense. This alone can usually make math quite a difference and kids will stay interested.
- Read through some fun math books, such as Theoni Pappas
 books, or puzzle-type books. Get to know some interesting math topics besides just schoolbook arithmetic. And, there are lots of story books (math readers) to teach math concepts - see a lists by concepts here.
books, or puzzle-type books. Get to know some interesting math topics besides just schoolbook arithmetic. And, there are lots of story books (math readers) to teach math concepts - see a lists by concepts here.
- Try including a bit about math history. This might work best in a homeschooling environment where there is no horrible rush to get through the thick book before the year is over. At LivingMath.net you can find a math history course designed for homeschoolers.
- When you use math in your daily life, explain how you're doing it, and include the children if possible. Figure it out together.
Miscellaneous Math Teaching tips
- The child needs to know the basic addition and multiplication facts very well, or she will have difficulties with fractions, decimals, etc. These basic facts need to be known by heart.
One of the best ways to start children with math is to have them skip-count up and down from a very young age. Use a number line to show what the 'skips' or steps mean. if your child can master the skip counting by twos, threes, fours, etc., she has learned a lot about addition and later on multiplication tables will be an easy fare! See also this article How to drill multiplication tables.
- Use manipulatives and pictures in your teaching. Almost all mathematical concepts can be illustrated with pictures, which can even take a place of concrete manipulatives. For example, if you can condition your child to draw lots of pie pictures when studying fractions, he/she can learn to visualize fractions as 'pies'. Then he/she won't make the addition mistake 1/2 + 1/4 = 2/6. Also certain kind of software can take place of the manipulatives.
- In geometry have your child or children DRAW a lot. See examples in the Math Mammoth Geometry ebook.
- When studying time, money, measuring, homeschoolers have an advantage since they can study those subjects in their natural settings. Involve your child when you measure, count money, check the time.
- In middle school years, it's important to get familiar with functions, relations, and patterns - these develop algebraic thinking. Check this article about algebraic reasoning from MathCounts.org.
- If you need to know the whys and wherefores of some particular math topic deeper than the textbook tells you, check Dr. Math's archives. The answers provided there are mathematically "sound doctrine", whereas math textbooks can contain all kinds of errors.
http://www.homeschoolmath.net/teaching/teaching.php

 )
) )
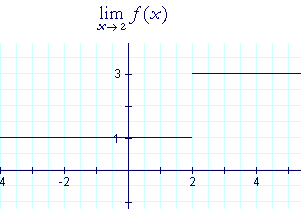
)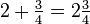 .
.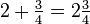 .
. for example is not a mixed number. Instead, multiplication is understood:
for example is not a mixed number. Instead, multiplication is understood:  .
. for example is not a mixed number. Instead, multiplication is understood:
for example is not a mixed number. Instead, multiplication is understood:  .
.
 value for
value for