Significant Figures
http://www.chem.tamu.edu/class/fyp/mathrev/mr-sigfg.html
There are two kinds of numbers in the world:
exact:
example: There are exactly 12 eggs in a dozen.
example: Most people have exactly 10 fingers and 10 toes.
inexact numbers:
example: any measurement.
If I quickly measure the width of a piece of notebook paper, I might get 220 mm (2 significant figures). If I am more precise, I might get 216 mm (3 significant figures). An even more precise measurement would be 215.6 mm (4 significant figures).
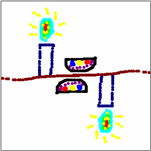
PRECISION VERSUS ACCURACY
Accuracy refers to how closely a measured value agrees with the correct value.
Precision refers to how closely individual measurements agree with each other.
accurate
(the average is accurate)
not precise
precise
not accurate
accurate
and
precise
The number of significant figures is the number of digits believed to be correct by the person doing the measuring. It includes one estimated digit.
So, does the concept of significant figures deal with precision or accuracy?
Conclusion: The number of significant figures is directly linked to a measurement.
So, does the concept of significant figures deal with precision or accuracy? Hopefully, you can see that it really deals with precision only. Consider measuring the length of a metal rod several times with a ruler. You will get essentially the same measurement over and over again with a small reading error equal to about 1/10 of the smallest division on the ruler. You have determined the length with high precision. However, you don't know if the ruler was accurate to begin with. Perhaps it was a plastic ruler left in the hot Texas sun and was stretched. You don't know the accuracy of your measuring device unless you calibrate it, i.e. compare it against a ruler you knew was accurate. Note: in the laboratory, a good analytical chemist always calibrates her volumetric glassware before using it by weighing a known volume of liquid dispensed from the glassware. By dividing the mass of the liquid by its density, she can determine the actual volume and hence the accuracy of the glassware.
Rules for Working with Significant Figures:
Leading zeros are never significant.
Imbedded zeros are always significant.
Trailing zeros are significant only if the decimal point is specified.
Hint: Change the number to scientific notation. It is easier to see.
The significant figures (also called significant digits) of a number are those digits that carry meaning contributing to its precision.
This includes all digits except:
.leading and trailing zeros where they serve merely as placeholders to indicate the scale of the number.
.spurious digits introduced, for example, by calculations carried out to greater accuracy than that of the original data, or measurements reported to a greater precision than the equipment supports.
The concept of significant digits is often used in connection with rounding. Rounding to n significant digits is a more general-purpose technique than rounding to n decimal places, since it handles numbers of different scales in a uniform way. For example, the population of a city might only be known to the nearest thousand and be stated as 52,000, while the population of a country might only be known to the nearest million and be stated as 52,000,000. The former might be in error by hundreds, and the latter might be in error by hundreds of thousands, but both have two significant digits (5 and 2). This reflects the fact that the significance of the error (its likely size relative to the size of the quantity being measured) is the same in both cases.
Computer representations of floating point numbers typically use a form of rounding to significant digits, but with binary numbers.
The term "significant digits" can also refer to a crude form of error representation based around significant-digit rounding; for this use, see significance arithmetic.
Identifying significant digits
The rules for identifying significant digits when writing or interpreting numbers are as follows:
All non-zero digits are considered significant. For example, 91 has two significant digits (9 and 1), while 123.45 has five significant digits (1, 2, 3, 4 and 5).
Zeros appearing anywhere between two non-zero digits are significant. Example: 101.12 has five significant digits: 1, 0, 1, 1 and 2.
Leading zeros are not significant. For example, 0.00052 has two significant digits: 5 and 2.
Trailing zeros in a number containing a decimal point are significant. For example, 12.2300 has six significant digits: 1, 2, 2, 3, 0 and 0. The number 0.000122300 still has only six significant digits (the zeros before the 1 are not significant). In addition, 130.00 has five significant digits. This convention clarifies the accuracy of such numbers; for example, if a result accurate to four decimal places is given as 12.23 then it might be understood that only two decimal places of accuracy are available. Stating the result as 12.2300 makes clear that it is accurate to four decimal places.
The significance of trailing zeros in a number not containing a decimal point can be ambiguous. For example, it may not always be clear if a number like 1300 is accurate to the nearest unit (and just happens coincidentally to be an exact multiple of a hundred) or if it is only shown to the nearest hundred due to rounding or uncertainty. Various conventions exist to address this issue:
A bar may be placed over the last significant digit; any trailing zeros following this are insignificant. For example, has three significant digits (and hence indicates that the number is accurate to the nearest ten).
The last significant digit of a number may be underlined; for example, "2000" has one significant digit.
A decimal point may be placed after the number; for example "100." indicates specifically that three significant digits are meant.[1]
However, these conventions are not universally used, and it is often necessary to determine from context whether such trailing zeros are intended to be significant. If all else fails, the level of rounding can be specified explicitly. The abbreviation s.f. is sometimes used, for example "20 000 to 2 s.f." or "20 000 (2 sf)". Alternatively, the uncertainty can be stated separately and explicitly, as in 20 000 ± 1%, so that significant-figures rules do not apply.
Scientific notation
Generally, the same rules apply to numbers expressed in scientific notation. However, in the normalized form of that notation, placeholder leading and trailing digits do not occur, so all digits are significant. For example, 0.00012 (two significant digits) becomes 1.2×10−4, and 0.00122300 (six significant digits) becomes 1.22300×10−3. In particular, the potential ambiguity about the significance of trailing zeros is eliminated. For example, 1300 to four significant digits is written as 1.300×103, while 1300 to two significant digits is written as 1.3×103.
Rounding
To round to n significant digits:
If the first non-significant digit is a 5 followed by other non-zero digits, round up the last significant digit (away from zero). For example, 1.2459 as the result of a calculation or measurement that only allows for 3 significant digits should be written 1.25.
If the first non-significant digit is a 5 not followed by any other digits or followed only by zeros, rounding requires a tie-breaking rule. For example, to round 1.25 to 2 significant digits, Round half up rounds up to 1.3, while Round half to even rounds to the nearest even number 1.2.
Replace any non-significant digits by zeros.
Arithmetic
Main article: Significance arithmetic
For multiplication and division, the result should have as many significant digits as the measured number with the smallest number of significant digits.
For addition and subtraction, the result should have as many decimal places as the measured number with the smallest number of decimal places.
When performing a calculation, do not follow these guidelines for intermediate results; keep as many digits as is practical to avoid rounding errors.[2]
Significant Figures and Rounding Rules
http://www.angelfire.com/oh/cmulliss/





 Line Bisector
Line Bisector Angle Bisector
Angle Bisector