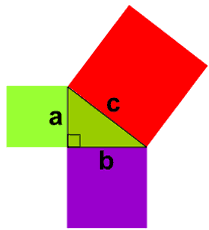
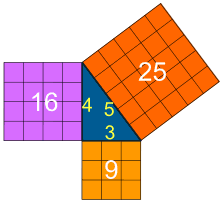
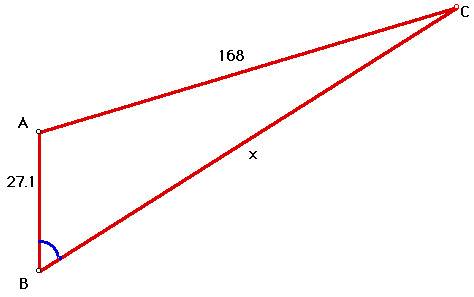
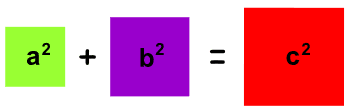The Rule of Four

The Rule of Four

Mathematics should be expressed in the following four ways:

1. Algebraically

2. Numerically

3. Graphically

4. Verbally

In order to understand mathematics holistically, it is important that students connect each concept with the rule of four.

Click Here

The beauty of this way of understanding mathematics is that it is so versatile; students can work with information presented in any one way and manipulate that information to find or interpret the information in other ways.

All students can learn

Three goals for the students:

1. Work accurately with basic operations:

2. Be able to apply basic operations to more complex problems.

3. Incorporate technology with the goal of higher level mathematics.

First and foremost my job is to ready my students for the next level of mathematics. Often, the level of mathematics dictates teaching methods.

When working with college-prep 9th graders in algebra, I focus heavily on a deep understanding of basic operations. The focus is essentially rote learning initially, and then we move to more involved problems. I teach and re-teach the basic skills that students will need to be successful when they reach algebra 2 and tackle the complexity therein.

When working with students in pre-calculus or calculus, I teach basic ideas fairly quickly and then move to complex applications of knowledge with the use of technology. I expose my students to the most rigorous IB or AP problems I can find or produce and sometimes much of class is spent discussing ideas rather than crunching numbers.

"In order to understand Math, you must do Math."

Having too much fun with the graphing calculator!

"Understanding of math is more than following examples.  It is the conceptual 'why' and 'how' and being able to apply that."

"The Rule of Three: Every topic should be presented geometrically, numerically and algebraically."

Mathematics Worksheets

Mathematics Worksheets

• Math-Drills
• Math-Aids

Quadratic Equation Application '-Distance Speed Time

Quotes on Mathematics

Quotes on Mathematics

True beauty is a matter of maths

MATHEMATICS – The music of reason

As G H Hardy had aptly put it: “a mathematician, like a poet or a painter is a maker of patterns and that if his patterns are more permanent than theirs, it is because they are made with ideas.” 

Expectation and Fair price

Expectation and Fair price

A person spins the pointer and is awarded the amount indicated by the pointer. 



It costs $8 to play the game. Determine: 


· The expectation of a person who plays the game.


· The fair price to play the game.

My work:
E=P(wins)(amount won)+P(loss)(amount lost)
E=1/3(-6)+2/3(-8)
E=1/3*-6/1 + 2/3*-8/1
E=-2/1+-16/3
E=-6/3+-16/3
E=-22/3=7.333
E=$7.33

Fair price=expectation + cost of play
Fair price= 7.33 +8.00
Fair price= $15.33

This just doesn't seem right to me, can someone tell me where I went wrong?

Riemann integral

In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of theintegral of a function on an interval.^[1] For many functions and practical applications, the Riemann integral can be evaluated by using the fundamental theorem of calculus or (approximately) by numerical integration.

The Riemann integral is unsuitable for many theoretical purposes. Some of the technical deficiencies in Riemann integration can be remedied with theRiemann–Stieltjes integral, and most disappear with the Lebesgue integral

The integral as the area of a region under a curve.

A sequence of Riemann sums over a regular partition of an interval. The number on top is the total area of the rectangles, which converges to the integral of the function.

The partition does not need to be regular, as shown here. The approximation works as long as the width of each subdivision tends to zero.

Average

In colloquial language average usually means the sum of a list of numbers divided by the size of the list, in other words the arithmetic mean. However it can alternatively mean the median, themode, or some other central or typical value. In statistics, these are all known as measures of central tendency.

Pythagorean means

The three most common averages are the Pythagorean means – the arithmetic mean, the geometric mean, and the harmonic mean.

Geometric mean can be thought of as the antilog of the arithmetic mean of the logs of the numbers.

Harmonic mean

reciprocal of the arithmetic mean of the reciprocals of the a_i's:

The mode has the advantage that it can be used with non-numerical data (e.g., red cars are most frequent), while other averages cannot.


Comparison of arithmetic mean, median and mode of twolog-normal distributions with different skewness.

Mathematics play a large role in our lives

“All things are numbers,” said Pythagoras, the Greek mathematician, philosopher and mystic 2600 years ago. To him, numbers brought order and harmony to everything, from cosmos to life to music.

He was, of course, right. We see numbers all around us, and we live our daily lives in numbers: Our medical reports and vital signs come in numbers, as do our businesses and finances. We check our calories, weights, driving speed, time, temperature and weather in numbers.

The West learned algebra and algorithm from the 1200-year old work of al-Khwarizmi, a Muslim mathematician. (Algebra comes from al-jabr in Arabic, and algorithm is the misspelled name of Khwarizmi.)

Pythagorean Triples

 If (a, b, c) is a Pythagorean triple, then so is (ka, kb, kc) for any positive integer k.

A "Pythagorean Triple" is a set of positive integers, a, b and c that fits the rule:

a² + b² = c²

Example: The smallest Pythagorean Triple is 3, 4 and 5.

3² + 4² = 5²

9 + 16 = 25

Here is a list of the first few Pythagorean Triples:

(3,4,5)	(5,12,13)	(7,24,25)	(8,15,17)	(9,40,41)
(11,60,61)	(12,35,37)	(13,84,85)	(15,112,113)	(16,63,65)
(17,144,145)	(19,180,181)	(20,21,29)	(20,99,101)	(21,220,221)
(23,264,265)	(24,143,145)	(25,312,313)	(27,364,365)	(28,45,53)
(28,195,197)	(29,420,421)	(31,480,481)	(32,255,257)	(33,56,65)
(33,544,545)	(35,612,613)	(36,77,85)	(36,323,325)	(37,684,685)
... infinitely many more ...

Scale Them Up

The simplest way to create further Pythagorean Triples is to scale up a set of triples.

Example: scale 3,4,5 by 2 gives 6,8,10

However, right triangles with non-integer sides do not form Pythagorean triples. For instance, the triangle with sides a = b = 1 and c = √2 is right, but (1, 1, √2) is not a Pythagorean triple because √2 is not an integer. Moreover, 1 and √2 do not have an integer common multiple because √2 is irrational.

Animation demonstrating the simplest case 

of the Pythagorean Triple: 3² + 4² = 5².

Endless

The set of Pythagorean Triples is endless.

It is easy to prove this with the help of the first Pythagorean Triple, (3, 4, and 5):

Let n be any integer greater than 1, then 3n, 4n and 5n would also be a set of Pythagorean Triple. This is true because:

(3n)² + (4n)² = (5n)²

Examples:

n	(3n, 4n, 5n)
2	(6,8,10)
3	(9,12,15)
...	... etc ...

So, you can make infinite triples just using the (3,4,5) triple.

Euclid's Proof that there are Infinitely Many Pythagorean Triples

However, Euclid used a different reasoning to prove the set of Pythagorean Triples is unending.

The proof was based on the fact that the difference of the squares of any two consecutive numbers is always an odd number.

Examples:

2² - 1² = 4-1 = 3 (an odd number),

15² - 14² = 225-196 = 29 (an odd number)

And also every odd number can be expressed as a difference of the squares of two consecutive numbers. Have a look at this table as an example:

n	n2	Difference
1	1
2	4	4-1 = 3
3	9	9-4 = 5
4	16	16-9 = 7
5	25	25-16 = 9
...	...	...

And there are an infinite number of odd numbers.

There is an infinite number of odd numbers. Since the perfect squares form a subset of the odd numbers, and a fraction of infinity is also infinity, it follows that there must also be an infinite number of odd squares. Therefore, there are an infinite number of Pythagorean Triples.

Properties

It can be observed that a Pythagorean Triple always consists of:

• all even numbers, or
• two odd numbers and an even number.

A Pythagorean Triple can never be made up of all odd numbers or two even numbers and one odd number. This is true because:

• (i) The square of an odd number is an odd number and the square of an even number is an even number.
• (ii) The sum of two even numbers is an even number and the sum of an odd number and an even number is in odd number.

Constructing Pythagorean Triples

It is easy to construct sets of Pythagorean Triples.

When m and n are any two positive integers (m < n):

• a = n² - m²
• b = 2nm
• c = n² + m²

Then, a, b, and c form a Pythagorean Triple.

Example: m=1 and n=2

• a = 2² - 1² = 4 - 1 = 3
• b = 2 × 2 × 1 = 4
• c = 2² + 1² = 5

Thus, we obtain the first Pythagorean Triple (3,4,5).

Similarly, when m=2 and n=3 we get the next Pythagorean Triple (5,12,13).

Importance Of Mathematics

Importance Of Mathematics

By Dr. Shakeel Ahmed Raina

In the Holy Quran God swears of even and odd numbers(Surah Al-Fajr, verse no.2). In fact in Holy Quran God swears of only important things for inculcating faith to mankind. Pythagoras (A famous ancient mathematician) asserted that numbers rule  the universe and unity is the essence of numbers. Our former Governor, Sh. S. K. Sinha has said in his address during the International Congress of Mathematics held in University of Jammu that mathematics is Queen of Sciences and Mother of all Technologies. An English mathematician George Boole developed the concept of Boolean Algebra in the year 1854. In 1938, it was observed by C.E. Shannon that Boolean algebra could be used to analyze switching (or electrical) circuits, which are used in the design of computer chips. Thus, Boolean algebra became an indispensable tool for the analysis and design of electronic computers in the succeeding decades. It is because of its immense applications mathematics in daily life, other subjects in general and science and technology in particular that our policy makers have introduced Applied Mathematics as a compulsory subject in 22 newly opened Colleges of the state during the session 2005-06. Some budding Universities in J&K have also started P.G Course of Applied Mathematics/ Mathematics on priority basis. It was the time when there were hardly one or two chapters of  statistics (which is also a branch of mathematics) and elementary mathematics in the syllabus of few science subjects and arts subjects. But today we see a big quantity of mathematics has been included in syllabus of many other subjects under different names like Econometrics  (the mathematics, used in economics), Biometry (the mathematics, used in bioscience), mathematics for Chemists (the mathematics, used in Chemistry), mathematics for physics (the mathematics, used in physics), Engineering Mathematics (the mathematics, used in engineering), Industrial Mathematics (the mathematics, used in industries), Mathematical Geography (the mathematics, used in geography), Commercial Mathematics, Computer Arithmetics, Biomathematics etc. Lot of interdisciplinary researches are going on in biomathematics in which people of sciences, medical doctors and mathematicians work jointly. One can see published papers and articles on the topics like “ Mathematical Coherence Behind Divine Verses” “Mathematics and Faith in God”, “Mathematics and Arrogance”, “ Communal harmony and Mathematics”, “Mathematics and Happiness”, Mathematics and Society” “Mathematics and Poetry” etc. From these topics and titles mentioned in above paragraph, one can easily guess that there is hardly any activity in which mathematics is not involved .I think at present a student  cannot study any subjects successfully without mathematics. In the words of J.W.A. Young, “wherever we turn in these days of iron, steam and electricity we find that mathematics has been the pioneer”. The position of our Country in mathematics at international level is very good. Our mathematicians like Aryabatta, Bhaskara, Bramagupta and Ramanujan have left indelible  imprints in the world of mathematics. Prof. L. T. Roczy while appreciating Indian’s contribution in mathematics has said. “There are many romantic notions in the heads of Europeans concerning India, but few know how essentially this country has contributed to the development of science in the western culture ever since ancient times. I just mention one fact; “Arabic numerals have reached Europe with the help of Arabic Scientists; the idea originated, however, from Indian. Even the use of ‘0’ for indicating an ‘empty’ position, did so” Our prime Minister Dr. Monmohan Singh during the speech while declaring December-22 as National Mathematics Day has said, “Mathematics seems to have acquired an independent identity as an intellectual discipline early on in human history. This identity became more sharply defined in the second half of the millennium before Christ, thanks to  major developments in Greece. In this period, India too made great strides in mathematics, though in ways very different from the Greeks. In the early centuries of the Common Era,  India was in fact in the lead in mathematical developments. Aryabhata in the fifth century, followed by Brahmagupta in the next are reckoned to be among the all-time great mathematicians. And we taught the world to think of zero as a number and the modern way of representing all numbers with 10 symbols. This arguably is the single most important mathematical development in all human history”. V. Krishnamurthy writes, “Ramanujan’s birth, his super activity in Madras and Cambridge, his glories rise and his unfortunate death all seem to have happened in a flash. He came and went like a meteor. When comes such another?” Ramanujan’s genius was ranked by the English mathematician G. H. Hardy in the same class as giants like Euler, Gauss, Archimedes and Newton. Our Hon’ble Prime Minister Dr. Monmohan Singh while declaring Ramanujan birth day (December 22) as national mathematics day said, Ramanujan, was extraordinary genius so very brightly lit up the world of  mathematics. Mathematics is a marvellous language of sciences. Mathematical language cuts short the  lengthy statements and puts them briefly, accurately and in exact form. For example we say  that path of projectile is y2 = 4ax, orbit of earth is x2/ a2 + y2/ b2 = 1, Ist, 2nd and 3rd equations of motions are v = u+ ft, s = ut+1/2ft and v2 = u2 + 2fs. The equation given by Einstein for atomic bomb is e = mc2. y = mx + c is a line and x2 + y2 = r2 is a circle, R2 is a plane and R3 is space. These are some of the simple examples on the basis of which we say that mathematics is a language.  One can easily verify that majority of the students is frighten of mathematics and take least  interest in this subject. Result of mathematics of schools particularly in remote areas almost remains below satisfactory. In my opinion mathematics is not a difficult subject because it is free from contradictions and it is simple subject because every concepts of mathematics has a single meaning not multi-meanings. What are the causes of this allergic attitude of students towards mathematics? As per my experience mathematics requires more time for  preparation as compared to other subjects. It is more time consuming subject and only those students can excel in mathematics who give it more and more time. But today we see that  majority of the students could not afford to spare sufficient time for mathematics because of their consumption of much time in attending private tuition centres, watching of television and involving themselves in several other activities. Secondly deficiency of mathematics teachers in schools is also one of the reasons of low performance of the students in mathematics and thirdly students are not properly motivated towards study of mathematics. Mahatma Gandhiji writes in Autobiography (page no.18) that he was not strong in geometry but when he reached to the thirteenth proposition of Euclid, the utter simplicity of the subject was suddenly revealed to him that a subject which only required a pure and simple use of  reasoning powers could not be difficult. Ever since that time geometry had become both easy and interesting for him. (Author is associate Professor and HOD Mathematics at Govt. Degree College ThannaMandi).

KITE

Kite

A quadrilateral with two distinct pairs of equal adjacent sides.


Area 
The area of a kite can be calculated in various ways. 

Area

Peremeter


A kite can become a rhombus 
In the special case where all 4 sides are the same length, the kite satisfies the definition of arhombus. A rhombus in turn can become a square if its interior angles are 90°.

Concave kites

If either of the end (unequal) angles is greater than 180°, the kite becomes concave. Although it no longer looks like a kite, it still satisfies all the properties of a kite.

Animation

Bearing

Bearing

(navigation)

In land navigation, bearing means the angle between a line connecting us and another object, and a north-south line. (ie, a meridian)

A standard Brunton Geo compass, used commonly by geologists and 

surveyors to obtain a bearing in the field.

Video Lecture on Bearing 

(IGCSE / O' Level)

Click Here to Watch Video on Bearing

Further Topics Study Required: Trigonometry

Problem

A pilot is flying at 168 mph. She wants her flight path to be on a bearing of 57 degrees and 40 minutes. A wind is blowing from the South at 27.1 mph. Find the bearing the pilot should fly, and find the plane's ground speed.

Hint:

Can you use the Law of Cosines to solve for x?

Then, use Law of Sines to solve for the angle at A.



 

The angle at B is 57 degrees and 40 minutes.

How Mathematicians Think