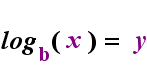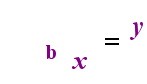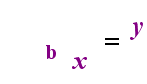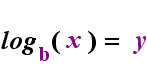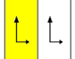List of Planar Symmetry Groups
Classes of discrete planar symmetry groups.
The symmetry groups are named here by three naming schemes: International notation, orbifold notation, and Coxeter's bracket notation.
There are three kinds of symmetry groups of the plane:
Rosette groups
There are two families of discrete two-dimensional point groups, and they are specified with parameter
n, which is the order of the group of the rotations in the group.
Frieze groups
The 7
frieze groups, the two-dimensional
line groups, with a direction of periodicity are given with five notational names. The
Schönflies notation
is given as infinite limits of 7 dihedral groups. The yellow regions
represent the infinite fundamental domain in each. Simple example images
are given as periodic tilings on a cylinder with a periodicity of 6.
[∞,1],   
[∞+,2],     
IUC
(Orbifold) |
Geo |
Schönflies |
Coxeter |
Fundamental
domain |
Example |
p11g
(∞x) |
p.g1 |
S2∞ |
[∞+,2+] |
 |
 |
p11m
(∞*) |
p.1 |
C∞h |
[∞+,2] |
 |
 |
|
[∞,2],     
IUC
(Orbifold) |
Geo |
Schönflies |
Coxeter |
Fundamental
domain |
Example |
p2
(22∞) |
p2 |
D∞ |
[∞,2]+ |
 |
 |
p2mg
(2*∞) |
p2g |
D∞d |
[∞,2+] |
 |
 |
p2mm
(*22∞) |
p2 |
D∞h |
[∞,2] |
 |
 |
|
Wallpaper groups
The 17
wallpaper groups, with finite fundamental domains, are given by
International notation,
orbifold notation, and
Coxeter notation, classified by the 5
Bravais lattices in the plane:
square, oblique (parallelogrammatic), hexagonal (60 degree rhombic), rectangular, and centered rectangular (rhombic).
The
p1 and
p2 groups, with no reflectional symmetry, are repeated in all classes. The related pure reflectional
Coxeter group are given with all classes except oblique.
- Square, [4,4],
    
IUC
(Orbifold) |
Geometric
Coxeter |
Fundamental
domain |
p1
(o) |
p1
[∞+,2,∞+] |
 |
p2
(2222) |
p2
[1+,4,4]+ |
 |
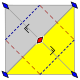
p2gg
pgg
(22x) |
pg2g
[4+,4+] |
 |
p2mm
pmm
(*2222) |
p2
[1+,4,4] |
 |
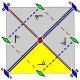
c2mm
cmm
(2*22) |
c2
[[4+,4+]] |
 |
p4
(442) |
p4
[4,4]+ |
 |
p4gm
p4g
(4*2) |
pg4
[4+,4] |
 |
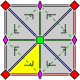
p4mm
p4m
(*442) |
p4
[4,4] |
 |
- Parallelogrammatic (oblique)
p1
(o) |
p1
[∞+,2,∞+] |
 |
p2
(2222) |
p2
[∞,2,∞]+ |
 |
|
- Hexagonal [6,3],
    
IUC
(Orbifold) |
Geometric
Coxeter |
Fundamental
domain |
p1
(o) |
p1
[∞+,2,∞+] |
 |
p2
(2222) |
p2
[∞,2,∞]+ |
 |
c2mm
cmm
(2*22) |
c2
[∞,2+,∞] |
 |
p3
(333) |
p3
[1+,6,3+] |
 |
p3m1
(*333) |
p3
[1+,6,3] |
 |
p31m
(3*3) |
h3
[6,3+] |
 |
p6
(632) |
p6
[6,3]+ |
 |
p6mm
p6m
(*632) |
p6
[6,3] |
 |
- Hexagonal [3[3]],
  
p3
(333) |
p3
[3[3]]+ |
 |
p3m1
(*333) |
p3
[3[3]] |
 |
p31m
(3*3) |
h3
[3[3[3]]+] |
 |
p6
(632) |
p6
[3[3[3]]]+ |
 |
p6mm
p6m
(*632) |
p6
[3[3[3]]] |
 |
|
List of spherical symmetry groups
Spherical symmetry groups are also called
point groups in three dimensions, however this article is limited to
the finite symmetries.
There are five fundamental symmetry classes which have triangular fundamental domains:
dihedral,
cyclic,
tetrahedral,
octahedral, and
icosahedral symmetry.
This article lists the groups by
Schoenflies notation,
Coxeter notation[1],
orbifold notation[2], and order.
John Conway
uses a variation of the Schoenflies notation, named by one or two upper
case letters, and whole number subscripts. The group order is defined
as the subscript, unless the order is doubled for symbols with a plus or
minus, "±", prefix.
[3]
Hermann–Mauguin notation (International notation) is also given. The
crystallography groups, 32 in total, are a subset with element orders 2, 3, 4 and 6.
Involutional symmetry
There are four
involutional groups: no symmetry,
reflection symmetry, 2-fold rotational symmetry, and central
point symmetry.
|
|
| Intl |
Geo |
Orbifold |
Schönflies |
Conway |
Coxeter |
Order |
Fundamental
domain |
| 1 |
22 |
× |
Ci
= S2 |
CC2 |
[2+,2+] |
2 |
 |
2
= m |
1 |
* |
Cs
= C1v
= C1h |
±C1
= CD2 |
[ ] |
2 |
 |
|
Cyclic symmetry
There are four infinite
cyclic symmetry families, with
n=2 or higher. (n may be 1 as a special case)
| Intl |
Geo |
Orbifold |
Schönflies |
Conway |
Coxeter |
Order |
Fundamental
domain |
| 2 |
2 |
22 |
C2
= D1 |
C2
= D2 |
[2]+ |
2 |
 |
| mm2 |
2 |
*22 |
C2v
= D1h |
CD4
= DD4 |
[2] |
4 |
 |
| 4 |
42 |
2× |
S4 |
CC4 |
[2+,4+] |
4 |
 |
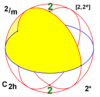
| 2/m |
22 |
2* |
C2h
= D1d |
±C2
= ±D2 |
[2,2+] |
4 |
 |
|
| Intl |
Geo |
Orbifold |
Schönflies |
Conway |
Coxeter |
Order |
Fundamental
domain |
3
4
5
6
n |
3
4
5
6
n |
33
44
55
66
nn |
C3
C4
C5
C6
Cn |
C3
C4
C5
C6
Cn |
[3]+
[4]+
[5]+
[6]+
[n]+ |
3
4
5
6
n |
 |
3m
4mm
5m
6mm
- |
3
4
5
6
n |
*33
*44
*55
*66
*nn |
C3v
C4v
C5v
C6v
Cnv |
CD6
CD8
CD10
CD12
CD2n |
[3]
[4]
[5]
[6]
[n] |
6
8
10
12
2n |
 |
3
8
5
12
- |
62
82
10.2
12.2
2n.2 |
3×
4×
5×
6×
n× |
S6
S8
S10
S12
S2n |
±C3
CC8
±C5
CC12
CC2n / ±Cn |
[2+,6+]
[2+,8+]
[2+,10+]
[2+,12+]
[2+,2n+] |
6
8
10
12
2n |
 |
3/m
4/m
5/m
6/m
n/m |
32
42
52
62
n2 |
3*
4*
5*
6*
n* |
C3h
C4h
C5h
C6h
Cnh |
CC6
±C4
CC10
±C6
±Cn / CC2n |
[2,3+]
[2,4+]
[2,5+]
[2,6+]
[2,n+] |
6
8
10
12
2n |
 |
|
Dihedral symmetry
There are three infinite
dihedral symmetry families, with
n as 2 or higher. (
n may be 1 as a special case)
| Intl |
Geo |
Orbifold |
Schönflies |
Conway |
Coxeter |
Order |
Fundamental
domain |
| 222 |
2.2 |
222 |
D2 |
D4 |
[2,2]+ |
4 |
 |
| 42m |
42 |
2*2 |
D2d |
DD8 |
[2+,4] |
8 |
 |
| mmm |
22 |
*222 |
D2h |
±D4 |
[2,2] |
8 |
 |
|
| Intl |
Geo |
Orbifold |
Schönflies |
Conway |
Coxeter |
Order |
Fundamental
domain |
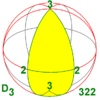
32
422
52
622 |
3.2
4.2
5.2
6.2
n.2 |
223
224
225
226
22n |
D3
D4
D5
D6
Dn |
D6
D8
D10
D12
D2n |
[2,3]+
[2,4]+
[2,5]+
[2,6]+
[2,n]+ |
6
8
10
12
2n |
 |
3m
82m
5m
12.2m |
62
82
10.2
12.2
n2 |
2*3
2*4
2*5
2*6
2*n |
D3d
D4d
D5d
D6d
Dnd |
±D6
DD16
±D10
DD24
DD4n / ±D2n |
[2+,6]
[2+,8]
[2+,10]
[2+,12]
[2+,2n] |
12
16
20
24
4n |
 |
6m2
4/mmm
10m2
6/mmm |
32
42
52
62
n2 |
*223
*224
*225
*226
*22n |
D3h
D4h
D5h
D6h
Dnh |
DD12
±D8
DD20
±D12
±D2n / DD4n |
[2,3]
[2,4]
[2,5]
[2,6]
[2,n] |
12
16
20
24
4n |
 |
|
Polyhedral symmetry
There are three types of
polyhedral symmetry:
tetrahedral symmetry,
octahedral symmetry, and
icosahedral symmetry, named after the triangle-faced
regular polyhedra with these symmetries.
[3,3]
| Intl |
Geo |
Orbifold |
Schönflies |
Conway |
Coxeter |
Order |
Fundamental
domain |
| 23 |
3.3 |
332 |
T |
T |
[3,3]+
= [3+,4,1+] |
12 |
 |
| m3 |
43 |
3*2 |
Th |
±T |
[3+,4]
= [[3,3]+] |
24 |
 |
| 43m |
33 |
*332 |
Td |
TO |
[3,3]
= [3,4,1+] |
24 |
 |
|
[3,4]
| Intl |
Geo |
Orbifold |
Schönflies |
Conway |
Coxeter |
Order |
Fundamental
domain |
| 432 |
4.3 |
432 |
O |
O |
[3,4]+
= [[3,3]]+ |
24 |
 |
| m3m |
43 |
*432 |
Oh |
±O |
[3,4]
= [[3,3]] |
48 |
 |
[3,5]
| Intl |
Geo |
Orbifold |
Schönflies |
Conway |
Coxeter |
Order |
Fundamental
domain |
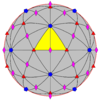
| 532 |
5.3 |
532 |
I |
I |
[3,5]+ |
60 |
 |
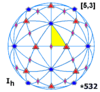
| 532/m |
53 |
*532 |
Ih |
±I |
[3,5] |
120 |
 |
|